Subtract mixed fractions

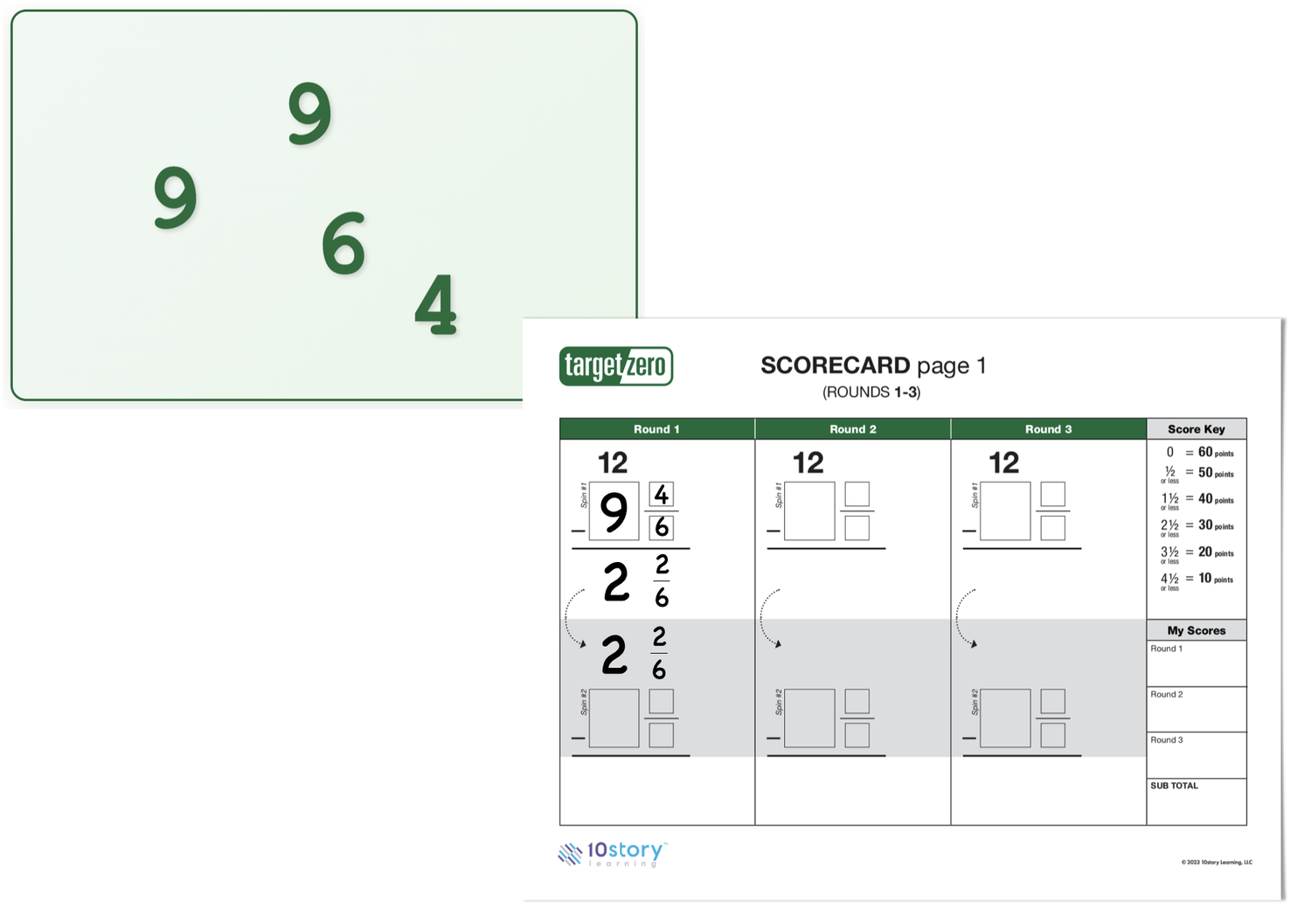
The game's central mechanic is construction under constraint. You get four random digits and must build a mixed fraction using three of them—one for the whole number, one for the numerator, one for the denominator. The constraint: numerator must be ≤ denominator. So with digits 2, 5, 7, 8, you could make 7⅝ or 5⅞ or 2⅞, but not 8⁷⁄₅. This forces students to think about what makes a valid fraction before they start computing.

Here's where it gets interesting mathematically. That constraint means students have to estimate magnitude on the fly. Is 7⅝ bigger than 5⅞? Well, 7⅝ is about 7.6 and 5⅞ is about 5.9, so yes. But notice that ⅞ is larger than ⅝ as a fraction, even though 5⅞ is smaller as a mixed number. Students start developing intuition about how the whole number and fractional parts contribute differently to overall size.

The subtraction happens in two stages. First, subtract your mixed fraction from 12. This often requires regrouping—if you're subtracting 8⅚ from 12, you need to rewrite 12 as 11⁶⁄₆ to handle the fractional part. Then you subtract a second mixed fraction from whatever you landed on. This two-step structure means students practice both "whole number minus mixed fraction" and "mixed fraction minus mixed fraction" in every round.

Common denominators come up constantly. If your first subtraction lands you at 3¾ and you need to subtract 1⅖, you're finding a common denominator for fourths and fifths. That's twentieths: 3¾ becomes 3¹⁵⁄₂₀, and 1⅖ becomes 1⁸⁄₂₀, giving you 1⁷⁄₂₀. Students who play regularly get fast at finding common denominators for the digit combinations that appear frequently.

Strategic play requires thinking ahead. If you make 8⅚ on your first draw, you'll subtract from 12 to get 3⅙. Now you need your second fraction to be as close to 3⅙ as possible. But you don't know what digits you'll get. Good players start developing a sense of which first-move fractions leave them flexible for the second subtraction. Sometimes making 6½ instead of 8⅚ gives you more options later.

The game naturally includes improper fractions and mixed number conversions. If a student lands on 1⁷⁄₅ after their first subtraction, they might convert it to 2⅖ before attempting the second subtraction. This back-and-forth between representations isn't explicitly taught—it emerges from students trying to make the computation easier.

What makes this pedagogically useful is the estimation-before-computation pattern. Students who jump straight to calculating often make errors and end up far from zero. Students who pause to estimate—"This should land me around 3, then subtracting about 2½ should get me close to ½"—tend to catch computational mistakes and score better. The game rewards the habit of checking whether your answer makes sense.

The most valuable habit Target Zero builds is estimation before computation. Students quickly learn that wild guessing about fraction size leads to scores of 6 or 8 when you're aiming for 0. Getting good at the game means getting good at mentally approximating: "⅞ is almost 1, so 5⅞ is almost 6, so 12 - 5⅞ should land around 6." This isn't abstract number sense—it's practical: better estimates lead to better scores.

The game also develops what you might call magnitude calibration with fractions. After a few rounds, students start internalizing that ⅞ is much larger than ⅛, that ⅗ sits somewhere in the middle, that ⁴⁄₅ and ⅚ are both pretty large but ⅚ is slightly bigger. This calibration happens through repeated exposure to different fractions and their effects on final scores, not through explicit instruction.

One pedagogically useful aspect is how the game separates strategic thinking from computational accuracy. You can be great at estimation and terrible at computing common denominators, or vice versa. Students start to see these as different skills that both matter. The kid who's fast with mental math but guesses randomly doesn't always beat the kid who's slow with computation but chooses fractions carefully.

Target Zero also provides built-in error detection. If you estimate you'll land on 1 but calculate 6⅓, something went wrong. Students develop the habit of sanity-checking their calculations against their predictions. This "does this answer make sense?" questioning is harder to teach directly but emerges naturally when wrong answers hurt your competitive position.

The constraint-based construction is worth noting pedagogically. The "numerator ≤ denominator" rule means students can't avoid thinking about fraction structure. They have to actively consider which digits can go where, which builds understanding of what makes a fraction valid. This is different from just being handed pre-made fractions to compute with.

Multi-round structure matters too. One bad round doesn't sink you—you play six rounds total. This teaches mathematical persistence: keep trying, refine your strategy, learn from mistakes. Students who get discouraged after one poor result in typical math exercises often stay engaged here because they have immediate opportunities to try again.

Finally, the game creates natural motivation for accuracy without external rewards. You want to get your subtraction right because you want to win, not because the teacher said so. This intrinsic motivation for precision is pedagogically valuable—it's students caring about correct computation for their own reasons.

Target Zero works best after students know how to subtract fractions with common denominators and how to find common denominators when needed. They should understand regrouping (borrowing from a whole number when the fractional part being subtracted is larger than what you have). If students are still shaky on these procedures, they'll spend all their time computing and won't engage with the strategic elements.

Groups of 2-4 work well. Pairs create intense head-to-head competition. Groups of 3-4 provide enough variety in strategies while keeping the game moving. Larger groups mean more waiting between turns, which can kill momentum. For whole-class play, run multiple small groups simultaneously rather than one large group.

First rounds typically go slowly. Students are learning both the game mechanics and working through unfamiliar fraction combinations. This is fine—let them work through it. Speed comes naturally after a few rounds as students recognize patterns and develop shortcuts. Rushing early rounds just creates confusion and errors.

Quick discussions between rounds help students learn from each other: "Who scored well this round? What fractions did you make?" Students start noticing that certain digit arrangements offer better opportunities, that sometimes a moderate first fraction works better than an extreme one. These insights spread through the group faster through peer discussion than through teacher explanation.

Watch for common errors in early play. Students who put larger numerators than denominators don't understand the constraint. Students who subtract denominators instead of finding common denominators need more work on fraction fundamentals. Students who forget to regroup need reminders to think about whether they have enough fractional parts to subtract. These errors tell you what needs additional instruction.

The scoring system does interesting things. Landing on ½ gets you 50 points—only 10 less than hitting zero exactly. This means students don't need perfection to score competitively. It also means smart students realize that aiming for ½ might be more reliable than aiming for zero. Discussions about scoring strategy reveal who understands fraction magnitude well.

Advanced players need additional challenges to stay engaged. Try: play with a different target (aim for 2 instead of zero), start from a different number (subtract from 15 instead of 12), or add a third subtraction per round. These variations maintain interest while providing additional fraction practice.

The six-round structure fits nicely into a 30-minute class period including setup and brief discussions. For longer sessions, students can play multiple complete games, tracking cumulative scores across games. This extended play lets students experiment with different approaches and refine strategies based on what worked in earlier games.

Assessment happens naturally during gameplay. You can see who computes accurately, who makes smart strategic choices, who struggles with specific subtraction types. Student scorecards provide written documentation of their work for later review. This beats traditional worksheets because students are computing for reasons they care about rather than just for points.

Post-game reflection questions: "What strategies helped you score well? When did you make good predictions? When did your calculations surprise you?" These questions help students articulate their thinking, making successful strategies explicit and transferable. Students who can explain why they chose certain fractions understand magnitude better than students who just got lucky.

Target Zero fits well into fraction units as practice that doesn't feel like practice. Students do dozens of mixed fraction subtractions per game, but they're not doing worksheets—they're competing. The repetition builds fluency, the strategy builds number sense, and the scoring provides immediate feedback on both. The activity drives the mathematics.