Use place value to round to 10 & 100

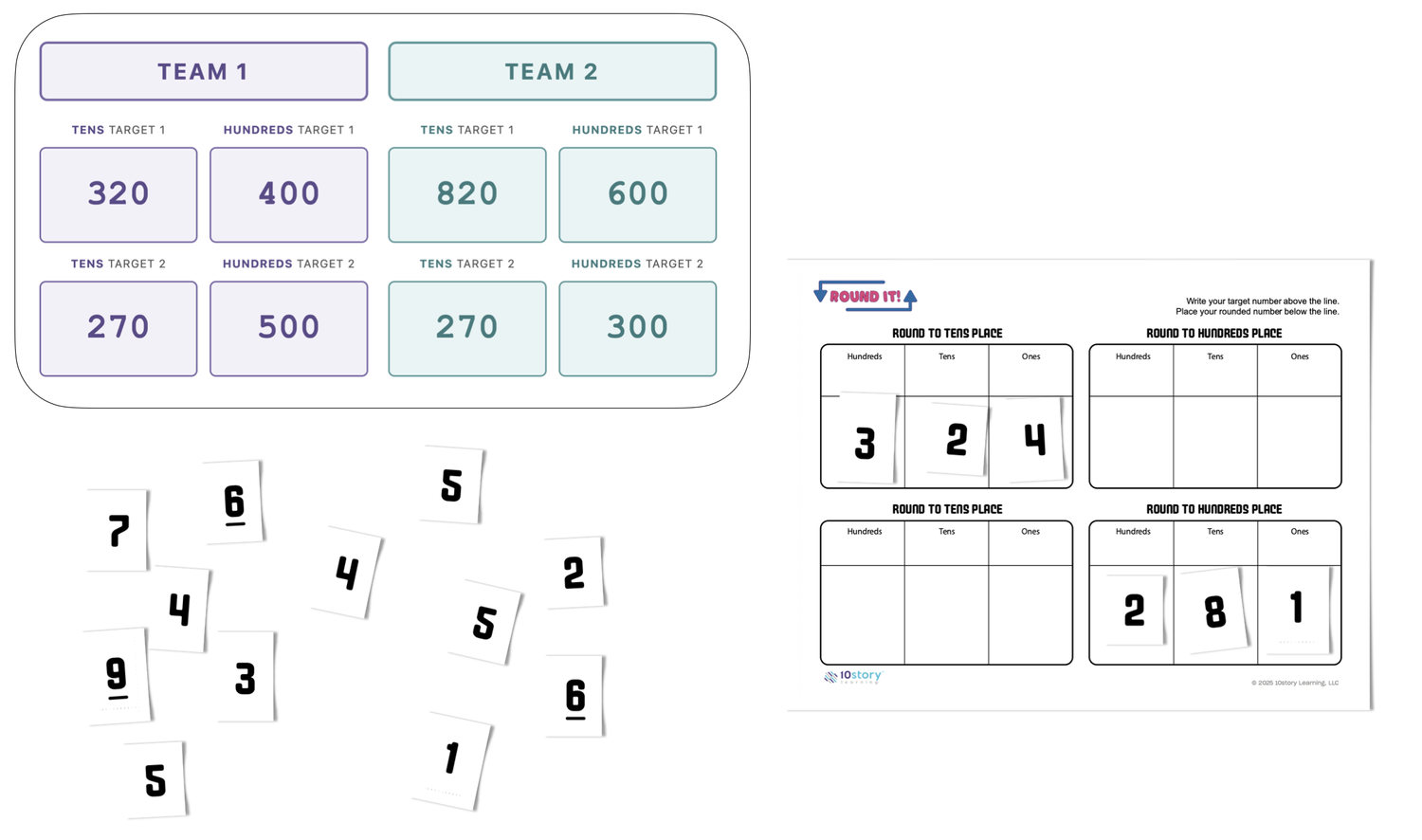
Most rounding practice asks students to take a number and round it—straightforward procedural work. Round It! reverses the task: given a target like 340, students must construct a three-digit number that rounds to it. This reversal requires understanding the range of qualifying numbers (335-344 for 340) rather than just applying a rule.

The game uses four targets per team: two require rounding to the nearest ten, two to the nearest hundred. Students must track which rounding place each target demands while managing a hand of five digit cards. On each turn, they select three cards to build a number that rounds to one of their targets.

Constructing numbers that round to specific targets reveals the relationship between place value and rounding outcomes.

Place value becomes consequential. When rounding to the nearest ten, the ones digit determines the direction (0-4 round down, 5-9 round up), but the tens digit tells you which decade you're approaching. For 347: the 4 in the tens place means you're in the 340s, and the 7 in the ones place rounds you up to 350. When rounding the same number to the nearest hundred, that 4 in the tens place now acts as the deciding digit, rounding down to 300.

Students work with digit cards 1-9, creating strategic tension. Holding 2, 3, 5, 7, 8, they might build 527 to hit a target of 530—but that 5 could be valuable later for rounding up in the hundreds place. These decisions require continuous mental evaluation of rounding possibilities across multiple targets.

Boundary cases appear naturally. Students quickly encounter situations where a number like 535 sits exactly between two multiples of ten. The standard convention (round 5 up) becomes meaningful through gameplay rather than memorization—when students realize that treating 535 as rounding to 540 gives them strategic flexibility, the convention makes practical sense.

The game also makes visible a common point of confusion: the difference between "the nearest multiple of 10" and "the nearest multiple of 100." Students see that 340 (nearest ten) and 300 (nearest hundred) require different numbers constructed from the same digit cards. Working with both types simultaneously builds flexibility rather than letting students conflate the two procedures.

The game builds mental math fluency through necessity. Students can't use calculators during competitive play, so they develop automatic recognition of rounding ranges. After several games, checking whether 347 rounds to 340 or 350 becomes instant rather than effortful—the kind of automaticity that frees cognitive resources for more complex mathematical work later.

Strategic thinking emerges from resource management. Students must evaluate trade-offs with incomplete information: use three strong cards now for one target, or save a valuable 5 for potential future plays? This forward planning, while mathematically lightweight, mirrors the kind of strategic thinking useful across problem-solving contexts.

Pattern recognition develops naturally. Students notice that targets ending in 0 (like 500) have wider qualifying ranges than targets like 540. Numbers from 495-504 all round to 500 (a 10-number range), while only 535-544 round to 540. This kind of noticing builds number sense—students start anticipating which targets will be easier or harder to match based on structural properties.

Verification at each step builds the metacognitive habit of asking "does this make sense?"

The game requires verification at each step. Before marking off a target, students must confirm their number rounds correctly. This self-checking habit—essential for mathematical independence—gets practiced dozens of times per game. Students develop the metacognitive skill of asking "does this make sense?" before committing to an answer.

Mathematical communication happens when teammates disagree about whether a number rounds correctly. Explaining why 347 rounds to 350 requires articulating the underlying logic, not just applying a rule. These explanatory moments deepen understanding for both the explainer and the listener.

The game also introduces an important mathematical concept implicitly: equivalence classes. All numbers from 535-544 are functionally equivalent for the purpose of rounding to 540, even though they're different numbers. This idea—that mathematical operations can treat different objects as equivalent—appears throughout later mathematics in fractions, modular arithmetic, and algebraic expressions.

Round It! works best as consolidation practice after initial rounding instruction. Students should already understand the basic procedure (check the digit to the right of the rounding place, round up if 5+, down if 4 or less) and recognize that three-digit numbers have hundreds, tens, and ones places. The game deepens this procedural knowledge into flexible understanding.

Materials are minimal: game mats, digit cards (printable), pencils, and the digital target generator. Teams of 1-2 players work well—pairs allow mathematical conversation between partners, while solo play builds individual fluency. Both formats serve different pedagogical purposes.

Common errors fall into two categories: rounding to the wrong place (building a number that rounds to 500 when they needed 540) or rounding incorrectly within the right place (claiming 347 rounds to 340 instead of 350). Both create teaching moments. When errors occur, ask students to explain their thinking—this often helps them identify where their reasoning went wrong.

Student errors reveal whether understanding is procedural or conceptual.

The 10-minute format maintains engagement while delivering 8-12 rounding decisions per team. For longer activities, run multiple rounds or tournament-style brackets. The game's replayability stays high—as students develop fluency, they play faster and appreciate the strategic depth more.

When students struggle to find qualifying numbers, guide their reasoning: "You need to round to 300. What digits in the tens place would round down? What range of numbers works?" This scaffolding helps students think about rounding ranges rather than guessing. Over multiple games, these reasoning patterns become internalized.

The discard option (discarding up to 3 cards when stuck) should be relatively rare. Frequent discarding suggests students don't understand rounding ranges well. If this happens, pause for explicit instruction: work through what numbers round to a specific target, then check whether current cards can build any of those numbers.

For struggling students, scaffolded versions help: start with only nearest-ten targets before introducing nearest-hundred targets, or play cooperatively (teams working together against time) rather than competitively. For advanced students, challenge them to identify all possible three-digit numbers that round to a given target, or find numbers that round to different values depending on place.

The game serves as effective formative assessment. Watching student gameplay reveals whether they understand rounding conceptually or are applying procedures mechanically. Students who consistently build incorrect numbers need additional conceptual instruction. Students who play correctly but slowly need more practice for fluency. Quick, accurate play indicates readiness for more advanced applications. The activity drives the mathematics.