Draw geometric figures

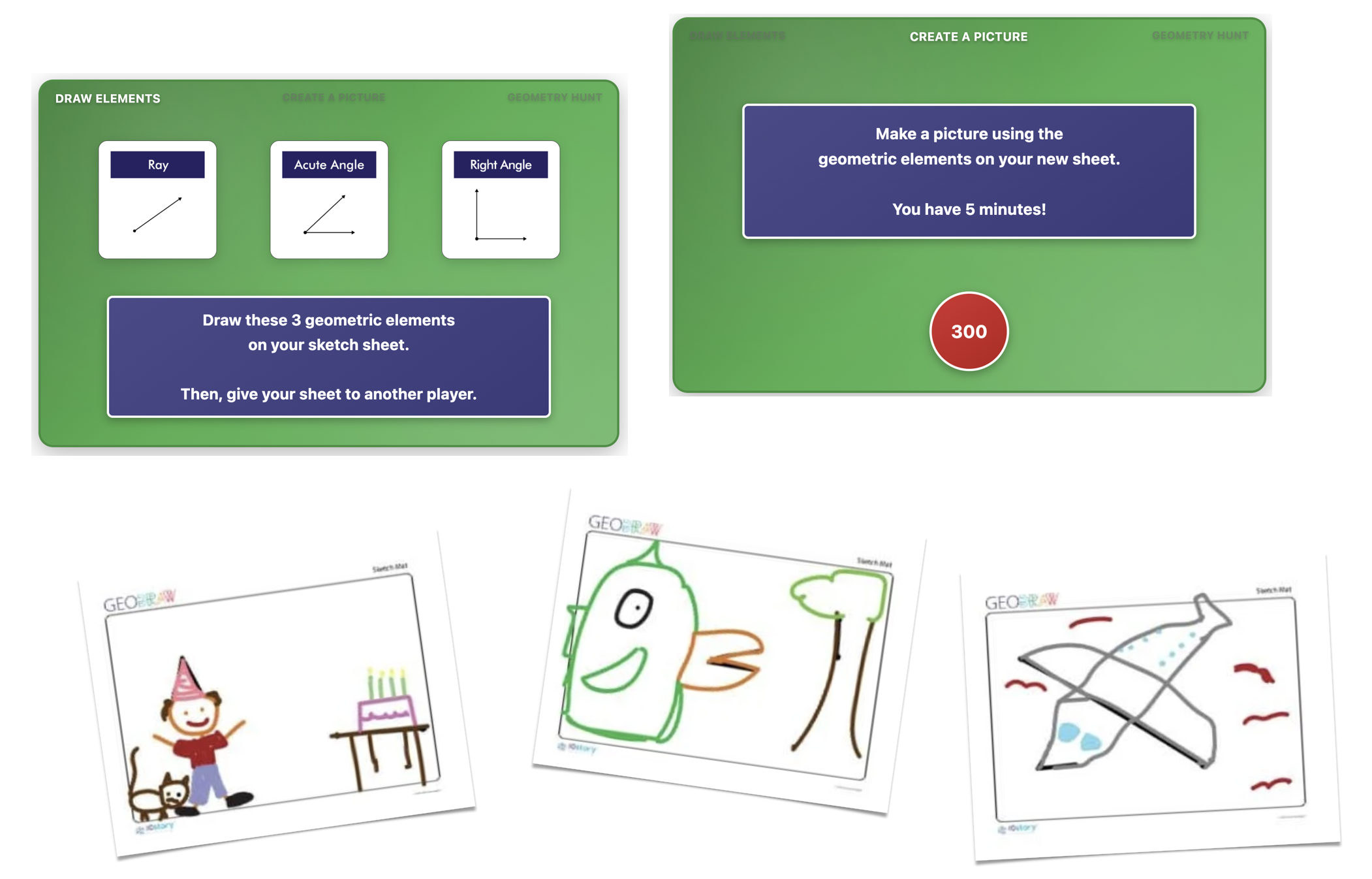
GeoDraw addresses a fundamental challenge in geometry education: students often learn **geometric terminology** in isolation from **visual recognition** and application. The game creates a context where students must both **produce geometric elements** deliberately and **identify them within complex compositions**—mirroring how geometric concepts appear in architecture, design, and the physical world.

The structure requires students to work with geometric elements in **three distinct cognitive modes**. First, they must draw specified elements—**translating formal definitions into precise visual representations**. A student who receives "acute angle" must recall that this means an angle measuring less than 90 degrees, then create that configuration. This production phase demands understanding of **defining properties**.

Second, students must **incorporate formal geometric elements into creative artwork**. When a student transforms a line segment into the edge of a building, or an acute angle into the prow of a ship, they're recognizing that geometric elements aren't just abstract objects but **foundational components of visual representation**. This integration challenges students to see **mathematical structures as building blocks**.

Third, students must **identify geometric elements within another student's artwork**. This visual search requires **recognizing familiar forms in unfamiliar contexts**. The acute angle that one student deliberately drew might appear as part of a tree, a roof, or a stylized letter. Students develop facility with **abstracting formal properties** from visual complexity—an essential geometric skill.

The game works with **fundamental geometric vocabulary**: points, line segments, rays, lines (infinite in both directions), and angle types (acute, obtuse, right, straight). Students must distinguish between related but distinct concepts. A line segment has two endpoints; a ray has one endpoint and extends infinitely; a line extends infinitely in both directions. These **distinctions matter** when identifying elements in drawings.

Angle classification requires students to **estimate angle measures visually**. An acute angle looks noticeably "sharp," opening less than a right angle. An obtuse angle appears "wider," opening more than 90 degrees but less than 180. Students develop **intuition about angle magnitude** through repeated practice identifying and classifying angles in varied orientations.

The game introduces **relationships between geometric elements**: parallel lines (never intersecting, always the same distance apart), perpendicular lines (intersecting at right angles), and intersecting lines (meeting at any angle). When students identify these relationships within drawings, they're recognizing **geometric properties that remain invariant** despite changes in orientation, scale, or artistic context.

Two-dimensional shapes emerge naturally as students create drawings. A triangle contains three line segments and three angles; a quadrilateral has four sides and four angles. Students begin recognizing that **shapes are defined by their geometric components**—sides, angles, vertices—and that these components can be identified even when embedded in complex images.

The collaborative nature means students see **multiple interpretations of the same requirements**. Given the same three elements, different students create vastly different artwork, yet all contain the specified geometric structures. This variation demonstrates that **geometric properties exist independently** of specific visual representations.

The game develops **geometric reasoning**—the ability to **recognize formal mathematical properties** in visual contexts and to **construct visual representations** from formal definitions. Through repeated practice creating and identifying geometric elements, students build connections between **geometric vocabulary, definitions, and visual appearance**.

The activity addresses a fundamental challenge: the **gap between knowing a definition and recognizing examples**. A student might correctly define an acute angle as "less than 90 degrees" yet struggle to identify acute angles in various orientations. The game provides practice **bridging this gap**, requiring students to find geometric elements where orientation, size, and artistic embellishment create visual complexity.

The activity builds understanding of **geometric precision** and the importance of definitions. When drawing a right angle, students must create two rays or segments that meet at exactly 90 degrees—not 85 or 95 degrees. This precision requirement helps students understand that **geometric terms have specific mathematical meanings**, not approximate or intuitive interpretations.

Students learn how **geometric elements combine to create complex structures**. Three line segments connected at their endpoints form a triangle; four segments create a quadrilateral. Students begin recognizing that **complex figures are built from simpler components**, and that analyzing these components reveals properties of the whole figure.

**Classification skills** develop through the identification phase. Students must distinguish between similar but distinct elements: line segment versus ray, acute versus right angle. These classification decisions require **careful attention to defining properties** and support **categorical thinking** essential throughout mathematics.

The collaborative aspect creates opportunities for **mathematical discussion and verification**. When one student identifies an element as a right angle and another questions whether it's truly perpendicular, they engage in **mathematical argumentation**—supporting claims with evidence, using vocabulary precisely, and refining understanding through dialogue.

The game builds **spatial reasoning and mental visualization**. Before drawing, students must imagine how geometric elements might combine in artwork. After viewing a finished drawing, they must **mentally decompose the image** to identify geometric components. This practice with **visual decomposition and composition** supports later work with transformations, constructions, and proofs.

The creative component demonstrates that **geometric thinking applies beyond mathematics class**. Architecture, graphic design, engineering, and art all require facility with geometric concepts. When students incorporate parallel lines into a cityscape or use acute angles to suggest motion, they experience **geometry as a practical tool** for visual communication.

**Pattern recognition** emerges as students play multiple rounds. Certain geometric elements appear frequently in particular types of drawings—perpendicular lines in buildings, acute angles in stars or arrows. Students begin anticipating where elements might appear and developing **strategies for systematic visual search**.

The game works well as **applied practice after introducing basic geometric vocabulary**: points, lines, line segments, rays, and angle types. It provides **contextualized repetition** where students use geometric terms repeatedly in purposeful activities rather than isolated drill.

Students should have **baseline familiarity with geometric definitions** before playing—understanding what distinguishes a line segment from a ray, knowing that angles are formed by two rays sharing an endpoint, recognizing basic angle categories. If students are still learning these concepts, begin with **simplified versions** using fewer geometric elements or focusing on just points, line segments, and basic angles.

**Group sizes affect the experience**. Pairs provide maximum drawing time and simplified passing. Groups of 3-4 work well for classroom implementation, creating variety while keeping wait times manageable. Larger groups (5-6) generate **diverse drawings** but require longer waits between participation.

Early gameplay benefits from **explicit discussion of what counts as each geometric element**. Establish class agreements: Does a line segment need to be straight? (Yes.) Can a wavy line count as a ray? (No—rays are straight.) Must angles show visible rays extending from the vertex? These clarifications prevent confusion and reinforce **precise geometric thinking**.

The initial drawing phase reveals **student understanding of geometric construction**. Observe whether students can accurately draw assigned elements: Do right angles look perpendicular? Are line segments truly straight? Do rays show clear direction? Student drawings provide **formative assessment data** about their grasp of geometric properties.

The five-minute art creation phase balances **creative freedom with time management**. This is sufficient for students to create recognizable artwork incorporating geometric elements without the game becoming unwieldy. Teachers can adjust timing based on students' drawing speed and engagement—some classes might need 7-8 minutes, others 3-4.

During identification, students may discover **ambiguous cases that spark mathematical discussion**: Is this angle exactly 90 degrees or slightly acute? Do these lines look parallel or nearly parallel? These situations create opportunities to discuss **geometric precision, measurement tools** (protractors, rulers), and the difference between approximate and exact relationships.

Some students will discover more geometric elements than others in the same drawing. This variation can prompt discussion: Why did one student identify 15 angles while another found 8? Did students use different criteria? Did some identify angles within shapes while others only found obvious angles? These discussions help students **refine their understanding** of what counts as a geometric element.

For students who finish quickly, **extension challenges** include: Find all instances of a specific element (count all acute angles), identify geometric relationships (find three parallel segments), or categorize elements by type (sort angles into acute, right, and obtuse). These extensions **deepen analysis** without requiring new materials.

Students struggling with identification benefit from **scaffolded support**: using colored pencils to circle different element types in different colors, working with a partner to verify identifications, or starting with simpler elements (points and line segments) before progressing to more complex ones (angle types and line relationships).

**Post-game discussion reinforces geometric concepts**. Ask: Which geometric elements were easiest to identify? Hardest? Why might parallel lines be harder to spot than right angles? Did anyone find elements that weren't originally drawn but emerged from the artwork? These discussions help students **articulate learning** and strengthen connections between **vocabulary and visual recognition**.

Multiple rounds allow students to encounter **different combinations of geometric elements** and create varied artwork. After several rounds, students develop **fluency with terminology** and increased speed in both drawing and identification phases. They also develop appreciation for how **geometric structures underlie visual compositions** in art, architecture, and design.

The game fits naturally into geometry units as **engaging practice with geometric vocabulary and visual recognition**. It provides purposeful application of geometric concepts in a creative context, making abstract geometric terms concrete through repeated visual production and identification. The activity drives the mathematics.