Work in the coordinate plane

Coordinate planes are everywhere: GPS navigation, computer screens, flight paths, city grids. The abstraction—representing two-dimensional position as an ordered number pair—underlies everything from video game programming to epidemiology mapping. But students often encounter coordinates as notation to memorize rather than as a representational tool that solves real spatial problems. 4Square turns coordinate plotting into strategic decision-making under constraint.

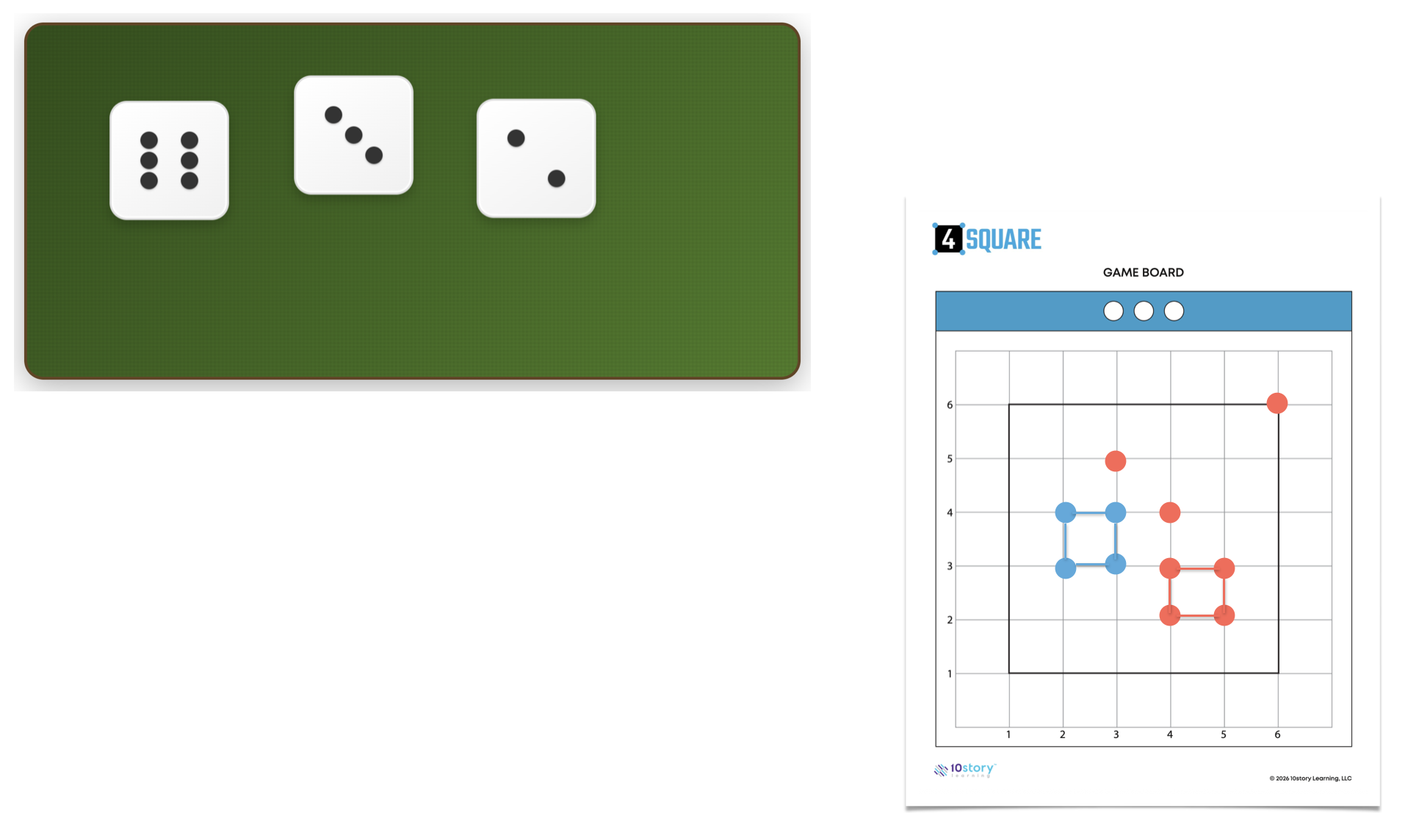
The core mechanic is simple. Roll three dice (say 2, 4, 6), pick any two to form an ordered pair, plot that point. The choice matters because some placements advance your own squares while others block your opponent. A point at (3, 4) might complete your square at corners (3, 4), (4, 4), (3, 5), (4, 5)—or it might be the only remaining corner your opponent needs to finish theirs. Students quickly internalize that (2, 5) and (5, 2) are not the same location, because plotting the wrong one might hand the game to their opponent.

Adjacency becomes concrete: two dots are horizontally adjacent if they share a y-coordinate and differ by 1 in x. Vertically adjacent means shared x-coordinate, difference of 1 in y. Students connect adjacent dots with line segments, building partial squares. After a few turns, the grid shows a network of connected and isolated points, and students must mentally project which combinations could become complete squares given their remaining dice possibilities.

The three circle trackers end the game when filled. If you roll combinations that are all occupied, you fill a circle instead of plotting. This happens more as the grid fills—a simple introduction to changing probability based on remaining outcomes. The trackers prevent the endgame from degenerating into frustrated rolling when most coordinates are taken.

The competitive structure does the pedagogical work. Students aren't plotting points because the worksheet says to—they're plotting because they need that corner or because blocking that coordinate wins the game. The coordinate plane stops being an abstract representation system and becomes a tool for spatial problem-solving. When a student plots (5, 3) to block an opponent's square, they're using coordinate geometry for strategic thinking, which is conceptually similar to how coordinates function in mapping, computer graphics, or any other applied context.

The pedagogical challenge with coordinate planes is that they're simultaneously simple (just count squares on a grid) and conceptually loaded (you're encoding 2D position as an ordered number pair using a conventionalized system). Students who mechanically plot points without understanding the underlying structure struggle when coordinate concepts reappear in algebra, geometry, and beyond.

4Square builds fluency through volume. Students plot 20-30 points per 10-minute game. Do that three times in a week and you've got nearly 100 coordinate placements—far more than typical worksheet practice, and students are motivated by competition rather than compliance. The repetition moves coordinate plotting from effortful decoding to automaticity, freeing cognitive resources for strategic thinking.

Spatial visualization develops alongside coordinate fluency. Before plotting, students must mentally project where (4, 5) will land and whether it advances their goals. This projection—translating ordered pairs into visualized positions—strengthens the bidirectional connection between symbolic representation and spatial reality. Strong players start seeing the grid as a tactical space rather than just a plotting surface.

Pattern recognition emerges organically. Students notice that completing squares requires four points in a rectangular pattern: (x, y), (x+1, y), (x, y+1), (x+1, y+1). After several games, they recognize partial squares automatically and identify missing corners. This is early algebraic thinking—understanding systematic relationships between coordinate values and spatial configurations.

The game naturally introduces coordinate transformations without calling them that. Moving from (3, 4) to (4, 4) means adding 1 to the x-coordinate—a horizontal translation. Moving from (3, 4) to (3, 5) means adding 1 to the y-coordinate—a vertical translation. These observations are foundational for later work with translations, functions, and algebraic reasoning about coordinate relationships.

Strategic thinking requires look-ahead. Strong players consider not just their current move but how it affects future options. This kind of consequential reasoning—if I plot here, then these squares become possible while those get blocked—appears throughout mathematics. It's the same cognitive move as "if I apply this operation, what properties will the result have?"

The game also makes coordinate constraints tangible. As the grid fills, options narrow. Certain positions become high-value because they participate in multiple potential squares. Students develop intuition about spatial scarcity and opportunity cost—concepts that extend well beyond coordinate geometry into probability, optimization, and strategic reasoning in general.

4Square works best after students know basic coordinate vocabulary (x-axis, y-axis, origin, ordered pair) but before they're fluent. You're looking for the zone where they can plot (3, 5) if they think about it, but they sometimes mix up the order or have to count carefully from the origin. The game builds fluency through motivated repetition.

Materials are minimal: game board (6 × 6 coordinate grid), two different colored markers, three dice. The digital dice roller on the website works fine if you're short on physical dice. Students play in pairs, and the 10-minute duration means you can easily run multiple rounds in a single period. Rotate partners between games—different opponents produce different strategic situations.

The square-completion rule needs emphasis initially. Some students shade squares prematurely or claim ownership without all four corners marked in their color. Establish the verification routine early: count all four corners, confirm they're all the same color, then shade. After a few disputes in early games, students internalize the standard.

First-time players often plot randomly, focused only on their own potential squares. By the third or fourth game, they start blocking opponent moves. Advanced players develop opening strategies—recognizing that certain initial placements create more square-building options than others. This progression happens naturally through play without explicit instruction.

The circle trackers provide a natural probability discussion. Early in the game, most rolls produce available coordinates. As the grid fills, more rolls yield only occupied positions. Students intuitively grasp that probability shifts based on remaining options. If you want to formalize it: with an empty 6 × 6 grid, what's the probability that a random three-dice roll produces at least one plottable ordered pair?

Students who struggle with plotting benefit from scaffolding: trace the x-axis with one finger, y-axis with another, move both to the intersection point. Or use different colored pencils to mark x and y separately before combining them. Some students need grids with darker lines or more explicit axis labels. Pair struggling students with confident plotters for peer support.

Post-game discussion makes learning explicit. Which dice rolls were most useful? Were corner positions (1,1) or (6,6) harder to incorporate into squares than middle positions? Did you notice patterns in which coordinates came up frequently? When did you block your opponent versus building your own squares? These reflections transform implicit strategic learning into articulated mathematical reasoning.

4Square scales up and down. For younger students or beginners, use a 4 × 4 grid with four-sided dice. For advanced students, extend to 8 × 8 or 10 × 10 grids, or require larger 2 × 2 squares instead of 1 × 1. Another variation: allow diagonal squares (corners at (1,1), (2,2), (1,3), (2,4) for example), which introduces distance calculations and non-axis-aligned geometric thinking.

The broader pedagogical point: coordinate planes appear throughout middle and high school mathematics—graphing linear equations, transforming geometric figures, representing functions, solving systems. Students who see coordinates only as abstract worksheet exercises often struggle when these concepts reappear. 4Square makes coordinates purposeful, positioning them as tools for spatial reasoning rather than arbitrary mathematical notation. That shift in understanding pays dividends later. The activity drives the mathematics.